Adam Ondra's bouldering flash grade
In this analysis, we explored the outdoor bouldering performance of world-renowned climber, Adam Ondra. Our data covers a period from 2008 to 2023 for grade V9 to V16, and was obtained from the climbing website 8a.nu.
The goal of our study is to examine the probabilities of Adam flashing (climbing successfully on the first attempt) boulders of various V-grades.
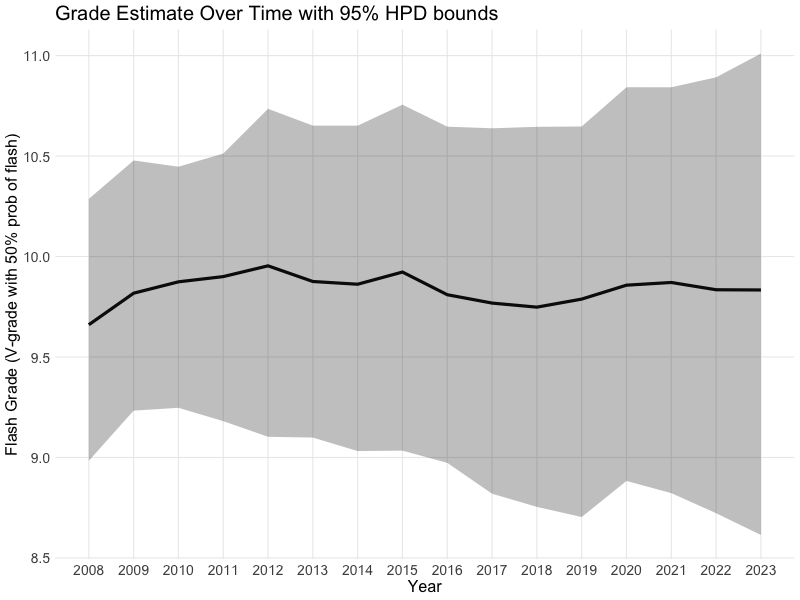
First, we performed a Bayesian logistic regression to estimate the “flash grade” (the highest grade where he has a 50% chance of flashing) and the “slope” (how quickly his flash probability decreases as the grade increases).
We assume that the slope (which is largely a intrinsic function of the grade scale) is constant over the period of time analysed, but that the flash-grade may change from year to year based on Ondra’s form and changes in training et cetera. We analyzed the data (see table below) on a year-by-year basis and used Bayesian inference to estimate the best fitting logistic function each year, where the slope was the same, but the flash grade could vary from one year to the next.
The first plot shows the estimated flash grade for each year from 2008 to 2023, along with the 95% HPD interval. This plot shows the remarkable consistency of performance that Ondra exhibited over this time period. Ondra’s estimated flash grade hovered between 9.5 and 10 throughout the whole time period.
Next, we compared the flash probabilities predicted by our model to the empirical proportion of boulders flashed (among those sent) for each V-grade. The plot shows the logistic curve based on the mean flash-grade from all 16 years of data and the fitted slope. The predicted flash probabilities from the model are shown in blue and they match very closely with the empirical proportion of boulders flashed by Ondra (in red) across the whole grade range analysed (V9-V16).
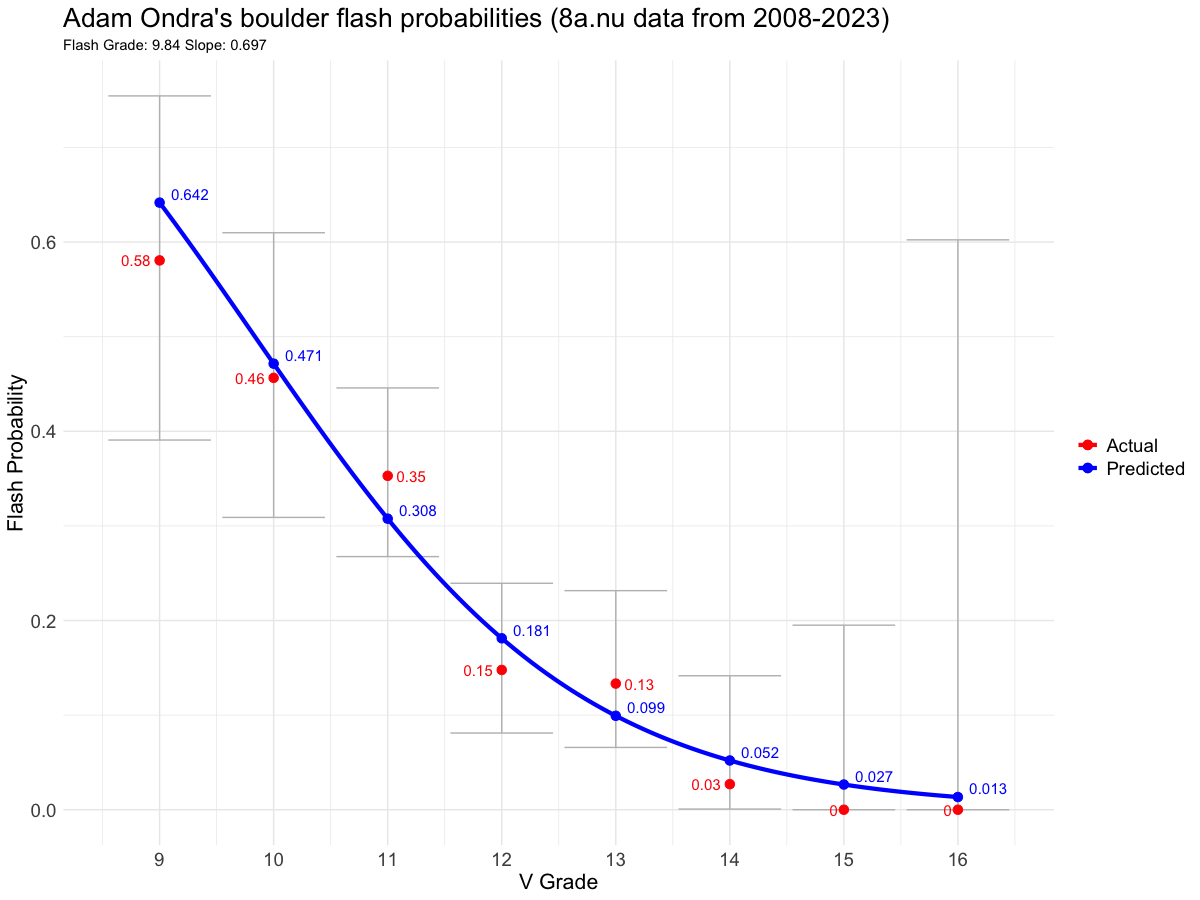
The blue line represents the flash probabilities predicted by our model, while the red dots represent the empirical proportion of boulders flashed of those sent.
Interestingly the slope that fits these data best is actually 0.696, for a multiplier of failed attempts per grade increment of $e^0.696 = 2.0$. This is significantly lower than the multiplier of 3.17 determined for a large cohort of amateur climbers and much closer to the multiplier of 2.1 found for sport climbing in the same study (Drummond and Popinga, 2021). This either reflects a different slope of the top-end bouldering grades more in line with sport climbing, or that elite climbers like Adam Ondra are more efficient with their tactics and effort and can translate their skills up the grades better than amateur climbers do at lower grades.
Below is a summary table of the data:
| V-grade | # flashed | # boulders sent | Proportion flashed | Model probability |
|---|---|---|---|---|
| 9 | 18 | 31 | 0.581 | 0.642 |
| 10 | 21 | 46 | 0.457 | 0.471 |
| 11 | 42 | 119 | 0.353 | 0.308 |
| 12 | 13 | 88 | 0.148 | 0.181 |
| 13 | 10 | 75 | 0.133 | 0.099 |
| 14 | 1 | 37 | 0.027 | 0.052 |
| 15 | 0 | 17 | 0.000 | 0.027 |
| 16 | 0 | 4 | 0.000 | 0.013 |
This analysis provides some interesting insights into Adam Ondra’s outdoor bouldering performance and may be useful for predicting his future performance, including the probability of flashing a V15.
As with any statistical analysis, it is based on a number of assumptions and simplifications, so results should be interpreted with caution.
 AscentStats
AscentStats